Abstract
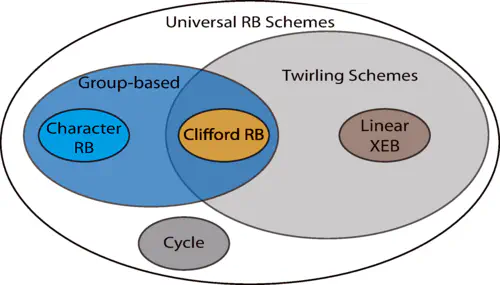
Randomized benchmarking (RB) is the gold standard for experimentally evaluating the quality of quantum operations. The current framework for RB is centered on groups and their representations, but this can be problematic. For example, Clifford circuits need up to $O(n^2)$ gates, and thus Clifford RB cannot scale to larger devices. Attempts to remedy this include new schemes such as linear cross-entropy benchmarking (XEB), cycle benchmarking, and non-uniform RB, but they do not fall within the group-based RB framework. In this work, we formulate the \emph{universal randomized benchmarking (URB) framework} which does away with the group structure and also replaces the recovery gate plus measurement component with a general ``post-processing’’ POVM. Not only does this framework cover most of the existing benchmarking schemes, but it also gives the language for and helps inspire the formulation of new schemes. We specifically consider a class of URB schemes called \emph{twirling schemes}. For twirling schemes, the post-processing POVM approximately factorizes into an intermediate channel, inverting maps, and a final measurement. This leads us to study the twirling map corresponding to the gate ensemble specified by the scheme. We prove that if this twirling map is strictly within unit distance of the Haar twirling map in induced diamond norm, the probability of measurement as a function of gate length is a single exponential decay up to small error terms. The core technical tool we use is the matrix perturbation theory of linear operators on quantum channels.